Efficiency

Memoization

Remember the results that have been computed before.

The below memo decorator takes in a function and only calls it when the result of f(n) is not found in cache. It only behave the same as f if f is pure.

def memo(f):
    cache = {}
    def memoized(n):
        if n not in cache:
            cache[n] = f(n) # Only call f when the result of f(n) is not found
        return cache[n]
    return memoized

Orders of Growth

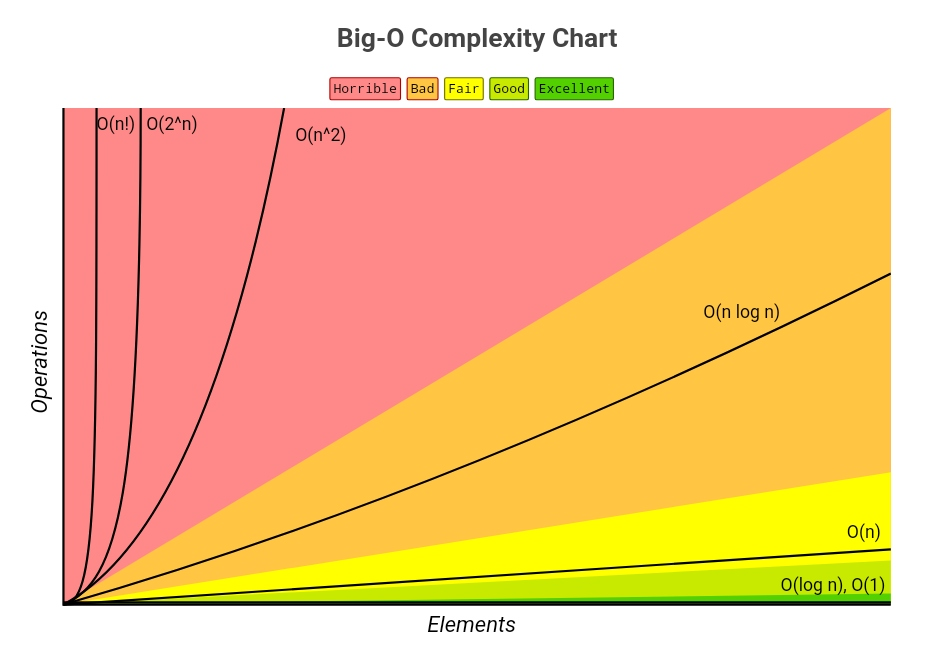
The order of growth of a process expresses in simple terms how the resource (computational resources of space and time) requirements of a process grow as a function of the input. Processes can be catagorized according to the order of growth.

A few examples

Category	Theta Notation	Growth Description	Example	Equation - Left: Time for input $n+1$ - Right: Time for input $n$
Constant	$$\Theta,(1)$$	Growth is independent of the input	abs Dictionaries
Logarithmic	$$\Theta,(\log n)$$	Doubling $n$ increments time by a constant	fast_exp	- Left: Time for $n+n$ $$a\cdot \ln(2\cdot n) = (a\cdot \ln n)+ a\cdot \ln 2$$
Linear	$$\Theta,(n)$$	Incrementing $n$ increases time by a constant	exp	$$a\cdot (n+1) = (a\cdot n) + a$$
Quadratic	$$\Theta,(n^2)$$	Incrementing $n$ adds time by $n$ times a constant	one_more	$$a\cdot (n+1)^2 = (a\cdot n^2)+a\cdot(2n+1)$$
Exponential	$$\Theta,(b^n)$$	Incrementing $n$ multiplies time by a constant	fib	$$a\cdot b^{n+1} = (a\cdot b^n)\cdot b$$

Example: Exponentiation

This is a simple impementation of exponentiation, which doubles the multiplication when doubled the problem size.

$$b^n=\{\begin{array}{ll}1& \text{if }n=0\\ b\cdot b^{n-1}& \text{otherwise}\end{array}$$

def exp(b, n):
    if n == 0:
        return 1
    else:
        return b * exp(b, n-1)

This implementation takes Linear time:

• Doubling the input doubles the time
• $1024\times$ the input takes $1024\times$ as much time

---

One more multiplication lets us double the problem size.

$$b^n=\{\begin{array}{ll}1& \text{if }n=0\\ {\left(b^{\frac{1}{2}n}\right)}^2& \text{if }n\text{ is even}\\ b\cdot b^{n-1}& \text{if }n\text{ is odd}\end{array}$$

def exp_fast(b, n):
    if n == 0:
        return 1
    elif n % 2 == 0:
        return square(exp_fast(b, n//2))
    else:
        return b * exp_fast(b, n-1)


def square(x):
    return x * x

This implementation takes Logarithmic time:

• Doubling the input increases the time by a constant $C$
• $1024\times$ the input increases the time by only 10 times $C$

Quadratic Time

Functions that process all pairs of values in a sequence of length $n$ take quadratic time.

e.g.

def overlap(a, b):
    count = 0
    for item in a:
        for other in b:
            if item == other:
                count += 1
    return count

Exponential Time

Tree-recursive functions can take exponential time.

e.g. non-memorized fib

Order of Growth Notation

Big O Notation $O$

It is defined as upper bound and upper bound on an algorithm is the most amount of time required ( the worst case performance).

Big Theta Notation $\mathrm{\Theta }$

It is define as tightest bound and tightest bound is the best of all the worst case times that the algorithm can take.

Space, Memory

In evaluating an expression, the interpreter preserves all active environments and all values and frames referenced by those environments. An environment is active if it provides the evaluation context for some expression being evaluated. An environment becomes inactive whenever the function call for which its first frame was created finally returns.

Python automatically reclaim inactive frames.

>>> def count_frames(f):
        def counted(*args):
            counted.open_count += 1
            counted.max_count = max(counted.max_count, counted.open_count)
            result = f(*args)
            counted.open_count -= 1
            return result
        counted.open_count = 0
        counted.max_count = 0
        return counted

>>> fib = count_frames(fib)
>>> fib(19)
4181
>>> fib.open_count
0
>>> fib.max_count
19
>>> fib(24)
46368
>>> fib.max_count
24

To summarize, the space requirement of the fib function, measured in active frames, is one less than the input, which tends to be small. The time requirement measured in total recursive calls is larger than the output, which tends to be huge.