8.1 多元函数基本概念

$n$ 维点集

与 ${\mathbb{R}}^3$ 空间类似，所有 $n$ 元有序数组 $(x_1,x_2,\cdots ,x_n)$ 的集合在赋予了加法和数乘运算后称为 $n$ 维线性空间，记为 ${\mathbb{R}}^n$；$(x_1,x_2,\cdots ,x_n)$ 称为 $n$ 维向量，常记为

$$x=(x_1,x_2,\cdots ,x_n)$$

其中 $x_1,x_2,\cdots ,x_n$ 称为向量 $\mathit{x}$ 的坐标或分量 定义向量的模为：

$$||\mathit{x}||={\left(\sum _{i=1}^n{x}_i^2\right)}^2$$

向量与 $n$ 维坐标轴的点一一对应，可称为 ${\mathbb{R}}^n$ 中的点，记为 $P(x_1,x_2,\cdots ,x_n)$ 原点：$O(0,0,\cdots ,0)$ 两点间的距离：

$$d(P,Q)=\sqrt{(y_1-x_1{)}^2+(y_2-x_2{)}^2+\cdots +(y_n-x_n{)}^2}$$

特别地，在 ${\mathbb{R}}^2$ 中，

• 距离$$\mathrm{d}(P,P_0)=\sqrt{(x-x_0{)}^2+(y-y_0{)}^2}$$

多元函数中的充分小，定义更加严格，以下给出

$n$ 维空间的邻域

设 $P_0\in {\mathbb{R}}^n,\delta >0$，则有

• $P_0$ 的 $\delta$ 邻域：$$U(P_0,\delta )=\{P\mid P\in {\mathbb{R}}^n,d(P_0,P)<\delta \}$$
  • 不强调半径时，简记为 $U(P_0)$
• $P_0$ 的去心 $\delta$ 邻域：$$\stackrel{\circ }{U}(P_0,\delta )=\{P\mid P\in {\mathbb{R}}^n,0<d(P_0,P)<\delta \}$$

在 ${\mathbb{R}}^2$ 中，

• $P_0$ 的 $\delta$ 邻域$$U(P_0,\delta )=\{P(x,y)|\mathrm{d}(P,P_0)<\delta \}$$
  • 为圆域
• $P_0$ 的去心 $\delta$ 邻域$$\mathring{U}(P_0,\delta )=\{P(x,y)|0<\mathrm{d}(P,P_0)<\delta \}$$
• 距离的定义（二元函数）不同，决定了邻域的形状不同，若不加说明都为上述定义

在 ${\mathbb{R}}^3$ 中为球体域

内点、外点、边界

设集合 $E\subset {\mathbb{R}}^n,P_0\in {\mathbb{R}}^n$，做如下定义：

• 若 $\mathrm{\exists }\delta >0$, s.t. $U(P_0,\delta )\subset E$, 称 $P_0$ 为 $E$ 的内点
  • $E$ 的全体内点构成的集合称为 $E$ 的内部或内核，记为 $E^0$
• 若 $\mathrm{\exists }\delta >0$, s.t. $U(P_0,\delta )\cap E=\varnothing$, 称 $P_0$ 为 $E$ 的外点
• 若对 $\mathrm{\forall }\delta$, 在 $U(P_0,\delta )$ 内既有属于 $E$ 的点, 又有不属于 $E$ 的点, 称 $P$ 为 $E$ 的边界点
  • 其全体构成 $E$ 的边界, 记为 $\partial E$
• *若任一 $P_0$ 的邻域都含有 $E$ 中异于 $P_0$ 的点, 则称 $P_0$ 为 $E$ 的聚点
  • 全体聚点的集合称为 $E$ 的导集，记为 $E^{\prime }$. $E$的聚点可能属于 $E$, 也可能不属于 $E$

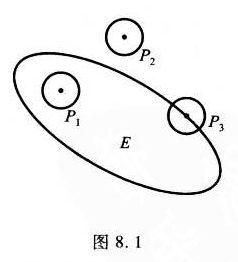
e.g. $\mathbb{R}$ 中的集合: 有理数

• 内点: 不存在 - 无理数是稠密的
• 外点: 不存在 - 有理数是稠密的
• 边界: $\mathbb{R}$

开集、闭集

请问开集和闭集如何理解？ - sola的回答 - 知乎

设集合 $E\subset {\mathbb{R}}^n$

• 若集合 $E$ 中每个点都是 $E$ 的内点, 称 $E$ 为 ${\mathbb{R}}^n$ 中的开集
• 开集 $E$ 的余集 ${\mathbb{R}}^n-E$ 称为闭集
• $E$ 的所有的边界点组成的集合称为 $E$ 的边界

性质:

• 空集和全集即开又闭
• $\partial E\subset E\iff E\text{是闭集}\iff E^{\prime }\subset E$

区域

设 $D\subset R^n$, 若 $D$ 中任意两点都能用完全属于 $D$ 的折线联结起来，则称 $D$ 是连通的

• 开区域: 连通的开集
  • 简称区域或开域
• 闭区域: 区域连同其边界

性质:

• 连通的闭集不一定是闭区域
  • 反例: $A=\{(x,y)|x^2+y^2\le 1\}\cup \{(x,y)|(x-2{)}^2+y^2\le 1\}$
• 闭区域不一定是连通的闭集 (${\mathbb{R}}^3$ 上的圆盘)
• ${\mathbb{R}}^n$ 上的 ${\mathbb{R}}^r(r<n)$ 维点集一定不是开集、闭集、开域、闭域

有界集和无界集

设集合 $E\subset {\mathbb{R}}^n$, $O$ 为 ${\mathbb{R}}^n$ 中的原点, 若 $\mathrm{\exists }M>0$, s.t. $E\subset U(O,M)$, 称 $E$ 为 ${\mathbb{R}}^n$ 中的有界集, 否则为无界集

• 有界的闭集不一定是闭域（非连续）

多元函数

函数依赖的自变量多于一个, 则称为多元函数

定义

设 $D$ 是 ${\mathbb{R}}^n$ 的非空集, $f$ 是 $D\to R$ 的映射 则称 $f$ 是定义在 $D$ 上的 $\mathit{n}$ 元函数, 记为

$$f:D\to R$$

或

$$u=f(P),P\in D$$

特别有二元函数:

$$z=f(x,y),f:D\to R,D\subseteq R^2$$

函数 $f$ 的定义域和值域

• 定义域 $D(f)$: 类似线性规划
• 值域 $R(f)$: 变量代换，转化为单元函数
• 自变量 $P$

多元初等函数

由不同变量的一元基本初等函数经过有限次四则运算和复合得到的函数