10.3 Green 公式及其应用

Green 公式

平面区域与边界曲线有关概念

连通区域

• 单连通区域 $D$ 内的任意一条封闭曲线所围成的区域都在 $D$ 内
• 复连通区域 则为相反

边界曲线的方向 动点沿区域 $D$ 的边界 $C$ 向一个方向前进时, 邻近处的 $D$ 总是在它的左侧, 此方向规定为闭曲线 $C$ 的正向. 赋予正向的边界曲线记为 $C^{+}$, 反之则为 $C^{-}$

格林公式 (定理)

设 $D$ 为平面有界闭区域, 其边界 $C$ 由分段光滑曲线组成 若函数 $P(x,y),Q(x,y)$ 在 $D$ 上有连续的偏导数, 则

$${\oint }_{C^{+}}P\mathrm{d}x+Q\mathrm{d}y={\iint }_D({\displaystyle \frac{\partial Q}{\partial x}}-{\displaystyle \frac{\partial P}{\partial y}})\mathrm{d}x\mathrm{d}y$$

• 2 -> 3
• 类似于牛顿莱布尼兹公式 1 -> 2

复连通区域 若 $D$ 是复连通区域, 格林公式的左端应当包含沿 $D$ 的全部边界的曲线积分 (正向)

用曲线积分表示区域面积 当 $P(x,y)=-y,Q(x,y)=x$, 则有 ${\displaystyle \frac{\partial Q}{\partial x}}-{\displaystyle \frac{\partial P}{\partial y}}=1$ 此时可以表示出曲面面积

$$A_D=\underset{D}{\iint }\mathrm{d}x\mathrm{d}y=-{\oint }_{C^{+}}y\mathrm{d}x=\underset{C^{+}}{\oint }x\mathrm{d}y={\displaystyle \frac{1}{2}}\underset{C^{+}}{\oint }x\mathrm{d}y-y\mathrm{d}x$$

非封闭曲线运用格林公式

对于非封闭的曲线, 考虑简单的曲线使之封闭 (头尾相连) 在应用格林公式简化计算

封闭区域积分 - 补上的定向曲线积分

奇点 (无定义点) 的处理

相见书和题集

环绕原点的一种特殊积分

设 $C$ 是任意一条不经过原点 $O$ 的光滑闭曲线, 并取逆时针方向, 则有

$${\oint }_C\frac{x\mathrm{d}y-y\mathrm{d}x}{x^2+y^2}=\{\begin{array}{ll}0,& \text{ 当 }C\text{ 不环绕原点 }\\ 2\pi ,& \text{ 当 }C\text{ 环绕原点 }\end{array}$$

向量形式的格林公式 (散度定理)

推导

若平面区域 $D$ 的正向边界曲线为 $C^{+}$, 函数 $\mathit{F}=(f(x,y),g(x,y))$ 在 $D$ 上有连续的偏导数

设与 $C^{+}$ 方向一致的单位切向量为 ${\mathit{e}}_{\tau }$, 单位外法向量为 ${\mathit{n}}^0$ 易得 ${\mathit{e}}_{\tau }=(\cos \alpha ,\cos \beta ),{\mathit{n}}^0=(\cos \beta ,-\cos \alpha )$

从而有第二类曲线积分的定义

$$(\mathit{F}\cdot {\mathit{n}}^0)\mathrm{d}s=f\cos \beta \mathrm{d}s-g\cos \alpha \mathrm{d}s=f\mathrm{d}y-g\mathrm{d}x$$

同时有

$$\mathrm{\nabla }\cdot \mathit{F}={\displaystyle \frac{\partial f}{\partial x}}+{\displaystyle \frac{\partial g}{\partial y}}$$

于是得到向量形式的格林公式

$${\oint }_{C^{+}}\mathit{F}\cdot {\mathit{n}}^0\mathrm{d}s=\underset{D}{\iint }\mathrm{\nabla }\cdot \mathit{F}\mathrm{d}\sigma$$

平面曲线积分与路径无关的条件

定义

我想这个可以用直观理解: 重力, 万有引力...

定义

设函数 $P(x,y),Q(x,y)$ 在区域 $D$ 内连续, 对 $D$ 内任意两点 $A,B$, 以及在 $D$ 内连接 $A,B$ 的任一条分段光滑曲线 $C$, 积分值 ${\displaystyle {\int }_{C}P\mathrm{d}x+Q\mathrm{d}y}$ 仅与 $C$ 的两端点 $A,B$ 有关

等价条件

设函数 $P(x,y),Q(x,y)$ 在单连通区域 $D$ 上有连续的偏导数, 则以下四个条件互相等价:

1. 对 $D$ 内的任一条分段光滑闭曲线 $C$, 有$${\oint }_{C}P\mathrm{d}x+Q\mathrm{d}y=0$$
2. 曲线积分 ${\displaystyle {\int }_{C}P\mathrm{d}x+Q\mathrm{d}y}$ 在 $D$ 内与路径无关
3. 存在 $D$ 上的可微函数 $u(x,y)$, 使得$$\mathrm{d}u=P\mathrm{d}x+Q\mathrm{d}y$$
4. 等式 ${\displaystyle \frac{\partial Q}{\partial x}}={\displaystyle \frac{\partial P}{\partial y}}$ 在 $D$ 内处处成立
   • 判断积分与路径无关的判据

解题技巧

1. 积分与路径无关, 通常取下列路径:
   • 平行坐标轴的直线段
   • 路径上没有奇点的直线段
   • 有利于被积函数简化的曲线
2. 实际解题时, 计算 ${\displaystyle \frac{\partial Q}{\partial x}}$ 和 ${\displaystyle \frac{\partial P}{\partial y}}$, 取相等部分, 则它们的积分与路径无关, 可简化计算 剩余部分按照第二类曲线积分的方法计算

全微分方程与全微分求积

全微分求积

求 $P\mathrm{d}x+Q\mathrm{d}y$ 的原函数的过程

单连通区域 $D$ 内具有连续偏导数的函数 $P(x,y),Q(x,y)$, 若在 $D$ 内恒成立等式

$$\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y},$$

那么微分式 $P\mathrm{d}x+Q\mathrm{d}y$ 在 $D$ 上存在原函数

原函数的形式 取定 $(x_0,y_0)\in D$,

$$u(x,y)={\int }_{(x_0,y_0)}^{(x,y)}P\mathrm{d}x+Q\mathrm{d}y,(x,y)\in D$$

全体原函数为

$$u(x,y)+C$$

全微分形式的 Newton-Leibniz 公式

类比: 保守力做功与路径无关, 只与始末位置有关

若 $u(x,y)$ 是 $P\mathrm{d}x+Q\mathrm{d}y$ 在 $D$ 上的一个原函数 对任意两点 $A(x_1,y_1),B(x_2,y_2)$, 或任取一条路径 $\stackrel{⏜}{AB}$, 有

$${\int }_A^{B}P\mathrm{d}x+Q\mathrm{d}y=u{|}_A^B=u(B)-u(A)$$

求全微分原函数方法

求出原函数, 就可以不管积分路径, 直接利用路径的始末位置求出曲线积分

**简化路径法** 若微分式 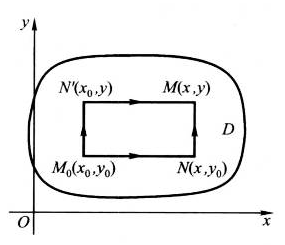$P\mathrm{d}x+Q\mathrm{d}y$ 存在原函数 $u(x,y)$, 则全微分求积可采用以下简化的方法: 取计算方便的折线段 $M_{0}NM$:

$$u(x,y)={\int }_{x_0}^{x}P(x,y_0)\mathrm{d}x+{\int }_{y_0}^{y}Q(x,y)\mathrm{d}y$$

或 $M_0{N}^{\prime }M$:

$$u(x,y)={\int }_{y_0}^{y}Q(x_0,y)\mathrm{d}y+{\int }_{x_0}^{x}P(x,y)\mathrm{d}x$$

待定函数法

例题 10.24 介绍的方法

设有存在原函数的全微分式 $P\mathrm{d}x+Q\mathrm{d}y$, $u(x,y)$ 为要求的原函数,

1. 由 ${\displaystyle \frac{\partial u}{\partial x}}=P(x,y)$, 于是有

   $$u(x,y)=\int P(x,y)\mathrm{d}x+C(y)$$
   • $C(y)$: 为仅关于 $y$ 的待定函数
   • ${\displaystyle \int P(x,y)\mathrm{d}x}$: 对 $x$ 求积分, 结果为一个关于 $x,y$ 的二元函数, 可记作 $R(x,y)$

2. 以上结果对 $y$ 求偏导,

   $${\displaystyle \frac{\partial u}{\partial y}}={\displaystyle \frac{\mathrm{d}}{\mathrm{d}y}}(\int P(x,y)\mathrm{d}x)+C^{\prime }(y)={\displaystyle \frac{\partial R}{\partial y}}+{\displaystyle \frac{\mathrm{d}C}{\mathrm{d}y}}=Q(x,y)$$

3. 通过比较系数得出 $C^{\prime }(y)$, 再求原函数得到 $C(y)+C$, 代入原式即得 $u(x,y)+C$ 为全体原函数

全微分方程

若 $P\mathrm{d}x+Q\mathrm{d}y$ 是某个二元函数 $u(x,y)$ 的全微分, 则称一阶微分方程

$$P(x,y)\mathrm{d}x+Q(x,y)\mathrm{d}y=0$$

为全微分方程

上述方程为全微分方程 $⟺$ 在某个单连通区域 $D$ 内满足 ${\displaystyle \frac{\partial Q}{\partial x}}={\displaystyle \frac{\partial P}{\partial y}}$. 而全微分方程的求解可以先求出 $P\mathrm{d}x+Q\mathrm{d}y$ 的一个原函数 $u(x,y)$, 然后就得到其通解 $u(x,y)+C$

非全微分方程的通解求法 若 $P(x,y)\mathrm{d}x+Q(x,y)\mathrm{d}y=0$ 不是全微分方程 (即 ${\displaystyle \frac{\partial Q}{\partial x}}\ne {\displaystyle \frac{\partial P}{\partial y}}$) 但当方程两端乘积分因子 $\mu (x,y)$ 后, 得到全微分方程:

$$\mu (x,y)P(x,y)\mathrm{d}x+\mu (x,y)Q(x,y)\mathrm{d}y=0$$

此时可以按照上面的方法求解

简单的积分因子可以观察得到

常见积分因子

$$\frac{1}{x^2},\frac{1}{y^2},\frac{1}{xy},\frac{1}{x^2+y^2},\frac{1}{x^2{y}^2},\frac{1}{\sqrt{x^2+y^2}}$$

常见构造

$$y\mathrm{d}x-x\mathrm{d}y:\{\begin{array}{l}{\displaystyle \frac{y\mathrm{d}x-x\mathrm{d}y}{y^2}}=\mathrm{d}\left({\displaystyle \frac{x}{y}}\right)\\ {\displaystyle \frac{y\mathrm{d}x-x\mathrm{d}y}{x^2}}=-\mathrm{d}\left({\displaystyle \frac{y}{x}}\right)\\ {\displaystyle \frac{y\mathrm{d}x-x\mathrm{d}y}{x^2+y^2}}=\mathrm{d}(\arctan {\displaystyle \frac{x}{y}})\\ {\displaystyle \frac{y\mathrm{d}x-x\mathrm{d}y}{xy}}=\mathrm{d}(\ln \left|{\displaystyle \frac{x}{y}}\right|)\end{array}$$