6.2 抽样检验
常用统计量的分布
正态分布
若随机变量
特别地, 当
- 均值的期望与方差
卡方分布 (正态总体的分布
设随机变量
其中 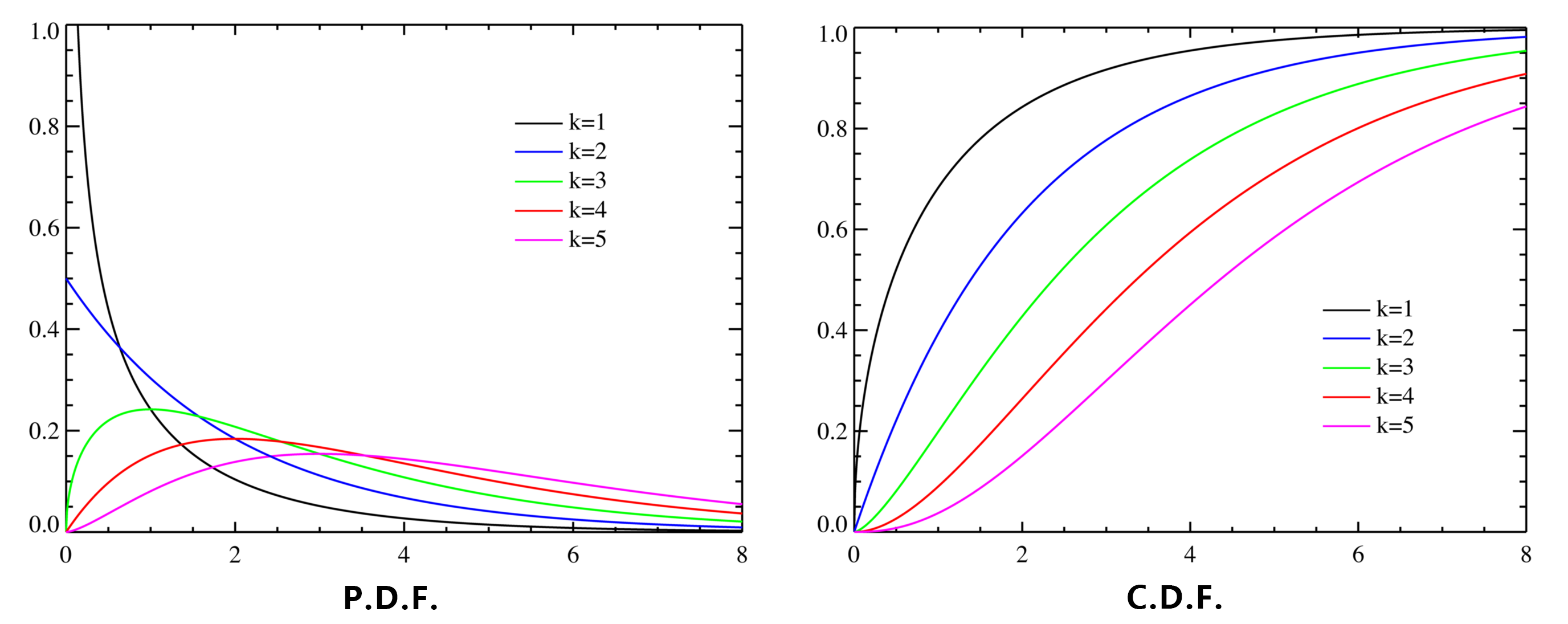
时, 为
性质
- 对于
, - 若
, 且两者相互独立, 则 - 当
很大时, 近似服从正态分布 的上侧 分位数 可查表
Gamma 函数的一些性质
t 分布
设

性质
分布的概率密度 为偶函数, 且当 时, 即当自由度
充分大时, 分布近似服从标准正态分布 当
时, 分布可用标准正态分布近似 分布的上侧 分位数 可查附表, 且
F 分布
设
其概率密度为
性质
- 若
, 则 的上侧 分位数 可查附表, 且