Caches

Summary

Cache Design Choices:

Size of cache: Speed vs. Capacity
Block (Line) size (cache aspect ratio)
Write Policy
Associativity choice of N
Block replacement policy
Write policy
Write miss policy
Cache levels

Memory Size

$2^{X Y}$ means

X = 1 => kibi ~ $10^{3}$
X = 2 => mebi ~ $10^{6}$
X = 3 => gebi ~ $10^{9}$
X = 4 => tebi ~ $10^{12}$
X = 5 => pebi ~ $10^{15}$
X = 6 => exbi ~ $10^{18}$
X = 7 => zebi ~ $10^{21}$
X = 8 => yobi ~ $10^{24}$
Y: Multiple of 2

Memory Hierarchy

A higher level contains data that is a subset of a lower level's memory data.

CPU Core, Registers
- Extremely fast
- Extremely expensive
- Tiny capacity
DRAM chip
- Fast
- Priced reasonably
- Medium capacity
Disk
- Slow
- Cheap
- Large

Mismatch between processor and memory speeds leads us to add a new level: introducing a "memory cache"

Memory Caching

Implemented with same IC processing technology as the CPU (usually integrated on same chip)
- Faster but more expensive than DRAM memory, and typically implemented with SRAM
- SRAM: Static Random Access memory
- DRAM: Dynamic Random Access Memory
Cache is (usually) copy of a subset of main memory
- Inclusive caching: Copying
- Exclusive caching: Moving the chunk from memory
Most processors have separate caches for instructions and data ⇒ I$, D$

If level closer to Processor, it is:
- Smaller
- Faster
- More expensive
- subset of lower levels (contains most recently used data)
Lowest Level (usually disk=HDD/SSD) contains all available data
Memory Hierarchy presents the processor with the illusion of a very large & fast memory

Cache Locality, Design, Management

Caches are an intermediate memory level between fastest and most expensive memory (registers) and the slower components (DRAM)
- DRAM can be considered a "cache" for caches/registers an disk in a way
Cache contains copies of data in memory that are being used.
Memory contains copies of data on disk that are being used.
Caches work on the principles of temporal and spatial locality.
- Temporal locality (locality in time): If we use it now, chances are we'll want to use it again soon.
- Spatial locality (locality in space): If we use a piece of memory, chances are we'll use the neighboring pieces soon.

Locality

Temporal Locality
- If a memory location is referenced then it will tend to be referenced again soon
- Keep most recently accessed data items closer to the processor
Spatial Locality
- If a memory location is referenced, the locations with nearby addresses will tend to be referenced soon
- Move blocks consisting of contiguous words closer to the processor

Cache Design

Three ways to organize cache (Associativity):
- Direct-mapped (everything in memory can only map to one location in a cache)
- Fully-associative (everything can go anywhere)
- N-way set associative (somewhere in between)
Multiple memory addresses map to the same cache location
Accessing memory data: Access cache first, if not found, go to memory
Quick locate: TIO (tag-index-offset) breakdown of the memory address

Managing Memory Hierarchy

registers << memory
- By compiler (or assembly level programmer)
cache << main memory
- By the cache controller hardware
main memory << disks (secondary storage)
- By the operating system (virtual memory)
- Virtual to physical address mapping assisted by the hardware ('translation lookaside buffer' or TLB)
- By the programmer (files)
- Also a type of cache

Effect of Caching

Caches provide an illusion to the processor that the memory is infinitely large and infinitely fast

Modern computers use multiple stages of caching, called multi-level caching, typically three levels: L1, L2, L3. The closer to the CPU, cache will become
- Faster
- Smaller
The effect of caching on performance
- In theory, caching boost performance
- In practice, there're times when things get worse (always need to go to the memory)

Multi-level Cache Block Size

Block sizes are usually equal across all levels of the cache hierarchy.

Direct Mapped Caches

In a direct-mapped cache, each memory address is associated with one possible block within the cache
- Therefore, we only need to look in a single location in the cache for the data if it exists in the cache
- Block is the unit of transfer between cache and memory

Example: 4 Byte Direct-Mapped Cache (Block size 1 byte)

Address   Memory     Cache Index  4 Byte
                                  Direct Mapped Cache
      0 ░░░░░░░░ ----------> 0 ░░░░░░░░
      1 ▒▒▒▒▒▒▒▒        |    1 ▒▒▒▒▒▒▒▒
      2 ▒▒▒▒▒▒▒▒        |    2 ▒▒▒▒▒▒▒▒
      3 ████████        |    3 ████████
      4 ░░░░░░░░ -------^
      5 ▒▒▒▒▒▒▒▒        |
      6 ▒▒▒▒▒▒▒▒        |
      7 ████████        |
      8 ░░░░░░░░ -------^
      9 ▒▒▒▒▒▒▒▒        |
      A ▒▒▒▒▒▒▒▒        |
      B ████████        |
      C ░░░░░░░░ -------^
      D ▒▒▒▒▒▒▒▒
      E ▒▒▒▒▒▒▒▒
      F ████████

Cache Location 0 can be occupied by the data from:
- Memory location 0, 4, 8, ...
- Any memory location that is multiple of 4
- LSB 2-bits

Example: 8 Byte Direct-Mapped Cache

Address   Memory      Cache Index  8 Byte
                                   Direct Mapped Cache
      0 ░░░░ ░░░░---------->  0 ░░░░ ░░░░
      2 ▒▒▒▒ ▒▒▒▒        |    1 ▒▒▒▒ ▒▒▒▒
      4 ▒▒▒▒ ▒▒▒▒        |    2 ▒▒▒▒ ▒▒▒▒
      6 ████ ████        |    3 ████ ████
      8 ░░░░ ░░░░ -------^    Block size = 2 bytes
      A ▒▒▒▒ ▒▒▒▒        |
      C ▒▒▒▒ ▒▒▒▒        |
      E ████ ████        |
     10 ░░░░ ░░░░ -------^
     12 ▒▒▒▒ ▒▒▒▒        |
     14 ▒▒▒▒ ▒▒▒▒        |
     16 ████ ████        |
     18 ░░░░ ░░░░ -------^
     1A ▒▒▒▒ ▒▒▒▒
     1C ▒▒▒▒ ▒▒▒▒
     1E ████ ████

When we ask for a byte, the controller finds the right block, and loads it all from memory
- Find the right block: Controller
- Select the right byte: check memory address LSB for which byte in block
- In practice, we select a word (32/64-bit)
Finding the right block: Applying a tag

Address   Memory      Cache Index  8 Byte
5-bit                              Direct Mapped Cache
      0 ░░░░ ░░░░        ---> 0| 1  ░░░░ ░░░░
      2 ▒▒▒▒ ▒▒▒▒        |    1| 0  ▒▒▒▒ ▒▒▒▒
      4 ▒▒▒▒ ▒▒▒▒        |    2| 2  ▒▒▒▒ ▒▒▒▒
      6 ████ ████  0     |    3| 3  ████ ████
      8 ░░░░ ░░░░ -------^    Block size = 2 bytes
      A ▒▒▒▒ ▒▒▒▒             ^            ^
      C ▒▒▒▒ ▒▒▒▒     Select index:   Select byte:
      E ████ ████  1    Middle 2-bits   LSB 1-bit
     10 ░░░░ ░░░░
     12 ▒▒▒▒ ▒▒▒▒
     14 ▒▒▒▒ ▒▒▒▒
     16 ████ ████  2
     18 ░░░░ ░░░░
     1A ▒▒▒▒ ▒▒▒▒
     1C ▒▒▒▒ ▒▒▒▒
     1E ████ ████  3 <--- Tag: MSB 2-bits of address

Tag: MSB 2-bits of the memory address, Cache number
- Indicating which chunk of memory (that is the same width of cache) does the block come from

Fields

32-bit address:
|ttttttttttttttttt|iiiiiiiii|oo|ooo|
Tag:    Check correct block
Index:  Select block
Offset: Get word/byte within block

Cache size: index_len (height) * offset_len (width)

Terminlogy

Memory address can be divided into three fields (read as unsigned integers)

Index
- specifies the cache index (which "row"/block of the cache we should look in)
Offset
- once we've found correct block, specifies which word/byte within the block we want
- Word offset: Selects which word in a block (for a Multiword-Block Direct-Mapped Cache)
- Byte offset: Selects byte within one word
Tag
- the remaining bits after offset and index are determined; these are used to distinguish between all the memory addresses that map to the same location

Memory Access with Cache

Example: Load word instruction: lw t0, 0(t1), t1 = 1022_ten, Memory[1022] = 99

Processor issues address 1022_ten to Cache
Cache checks to see if has copy of data at address 1022_ten (go to the cache index and check the tag)
- If finds a match (Hit): cache reads 99, sends to processor
- No match (Miss): cache sends address 1022 to Memory
  1. Memory reads 99 at address 1022_ten
  2. Memory sends 99 to Cache
  3. Cache loads a corresponding block (spatial locality) and replaces word with new 99
  4. Cache sends 99 to processor
Processor loads 99 into register t0

Caching Terminology

Cache cases:

Cache hit:
- cache block is valid and contains proper address, so read desired word
Cache miss:
- nothing in cache in appropriate block, so fetch from memory
Cache miss, block replacement:
- wrong data is in cache at appropriate block, so discard it and fetch desired data from memory (cache always copy)

Cache Temperatures:

Cold
- Cache empty
Warming
- Cache filling with values you'll hopefully be accessing again soon
Warm
- Cache is doing its job, fair percentage of hits
Hot
- Cache is doing very well, high percentage of hits

Cache Terms:

Hit rate: fraction of access that hit in the cache
Miss rate: 1 - Hit rate
Miss penalty: time to replace a block from lower level in memory hierarchy to cache
Hit time: time to access cache memory (including tag comparison)

Valid bit:

When start a new program, cache does not have valid information for this program
Need an indicator whether this tag entry is valid for this program
Add a "valid bit" to the cache tag entry
- 0 -> cache miss, even if by chance, address = tag
- 1 -> cache hit, if processor address = tag

Example: Multiword-Block Direct-Mapped Cache

Cache Write Policy

On write hit:

Write-throught
- Update both cache and memory (count as hit)
Write-back
- Update word in cache block
- Allow memory word to be 'stale'
- Add a 'dirty' bit to block, indicating
  - memory and cache inconsistent
  - needs to be updated when block is replaced
- OS flushes cache before I/O
Write-around
- Data is directly written to memory only
  - This often happens when data is only written and are not likely to be read again
  - Seen in databases
- Valid bit of the block changed to invalid
- No write 'hit' (no data at the address get fetched in cache)

Miss Policy:

Write-allocate
- On write miss, pull the block missed on into the cache
- Write-back, write-allocate memory: Memory is never written directly
No Write-allocate
- On write miss, no pulling, only memory is updated

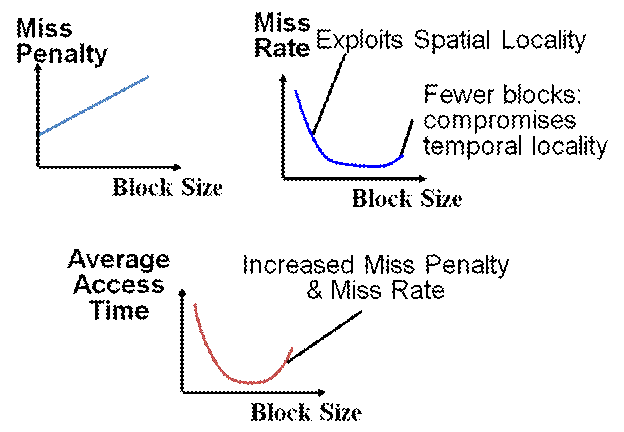
Block Size Tradeoff

Benefits of Larger Block Size
- Spatial Locality: if we access a given word, we’re likely to access other nearby words soon
- Very applicable with Stored-Program Concept
- Works well for sequential array accesses
Drawbacks of Larger Block Size
- Larger block size means larger miss penalty
  - on a miss, takes longer time to load a new block from next level
- If block size is too big relative to cache size, then there are too few blocks
  - Result: miss rate goes up (Ping Pong Effect: discard the last cache, and every cache access is a miss)

block_size_tradeoff_conclusion

Types of Cache Misses

"Three Cs" Model of Misses

Compulsory Misses
- occur when a program is first started
- cache does not contain any of that program’s data yet, so misses are bound to occur
- can’t be avoided easily
- Every block of memory will have one compulsory miss (NOT only every block of the cache)
- Solution:
  - increase block size (increases miss penalty; very large blocks could increase miss rate)
Conflit Misses
- miss that occurs because two distinct memory addresses map to the same cache location
- two blocks (which happen to map to the same location) can keep overwriting each other
- big problem in direct-mapped caches
- Solution:
  - increase cache size
  - increase associativity (may increase access time)
  - Improve replacement policy (LRU, ...)
Capacity Misses (general idea)
- miss that occurs because the cache has a limited size
- miss that would not occur if we increase the size of the cache
- primary type of miss for the Fully Associative Caches
- Solution:
  - increase cache size (may increase access time)

Catagorize Misses

Run an address trace against a set of caches:

First, consider an infinite-size, fully-associative cache. For every miss that occurs now, consider it a compulsory miss.
Next, consider a finite-sized cache (of the size you want to examine) with full-associativity. Every miss that is not in #1 is a capacity miss.
Finally, consider a finite-size cache with finite-associativity. All of the remaining misses that are not #1 or #2 are conflict misses.

Fully Associative Caches

Memory address fields:

Tag: same as before
Offset: same as before
Index: non-exsitant
- No "rows": any block can go anywhere in the cache
- must compare with all tags in entire cache to see if data is there

Fully Associative Caches procedure:

Compare tags in parallel
If found, check valid
If valid, that's a hit

Tradeoffs:

Benefits
- No conflit misses (data go anywhere)
Drawbacks
- Need hardware comparator for every single entry
- Must be small (otherwise comparator number is infeasible-4)

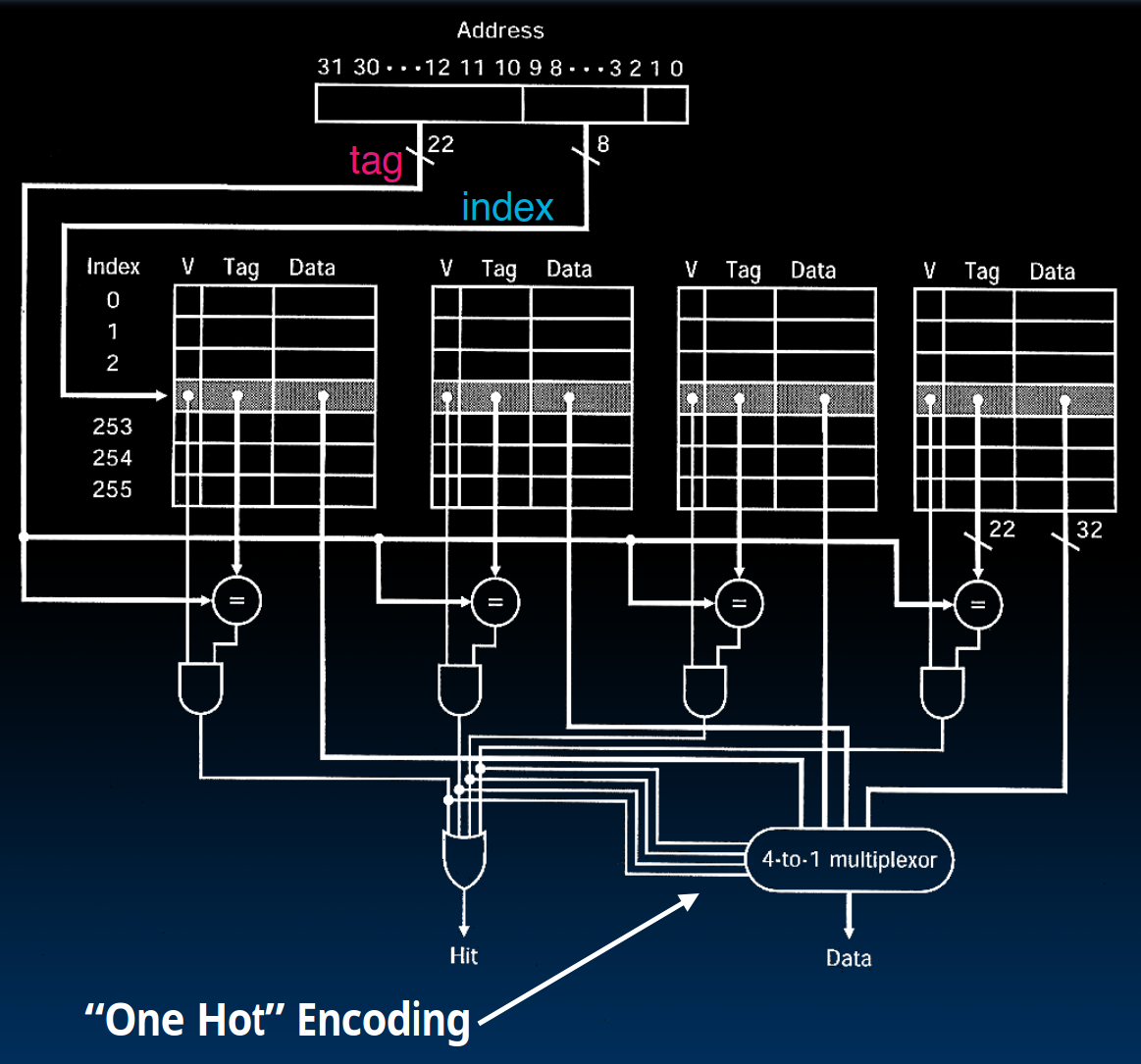
(N-Way) Set-Associative Caches

Memory address fields:

Tag: same as before
Offset: same as before
Index: point to the correct "row" (called a set)
- Each set contains multiple (N) blocks
- Once found the correct set, must compare with all tags in that set to find data
- Size of Cache = Number of sets * Number of blocks per set * Block size

Address  Memory         Cache Index
      0 ░░░░░░░░                  0 ░░░░░░░░
      1 ████████                  0 ░░░░░░░░
      2 ░░░░░░░░                  1 ████████
      3 ████████                  1 ████████
      4 ░░░░░░░░
      5 ████████
      6 ░░░░░░░░
      7 ████████

Given memory address, procedure to find a data:

Find correct set using Index value.
Compare Tag with all Tag values in that set.
If a match occurs, hit!, otherwise a miss.
Finally, use the offset field as usual to find the desired data within the block.

Benefits:

Avoids conflict misses
Only need N comparators

Difference with Direct-Mapped and Fully-Associative for a cache with M blocks:

If it's 1-way set assoc, it's direct-mapped
If it's M-way set assoc, it's fully assoc

Block Replacement

Direct-Mapped Cache
- index completely specifies position which position a block can go in on a miss
N-Way Set Assoc
- index specifies a set, but block can occupy any position within the set on a miss
Fully Associative
- block can be written into any position

Position to write an incoming block:

If there’s a valid bit off, write new block into first invalid.
If all are valid, pick a replacement policy

Replacement Policy

Rule for which block gets “cached out” on a miss.

LRU (Least Recently Used)
- Idea: cache out block which has been accessed (read or write) least recently
- Pro: temporal locality -> recent past use implies likely future use
- Con: with 2-way set assoc, easy to keep track (one LRU bit); with 4-way or greater, requires complicated hardware
FIFO
- Idea: ignores accesses, just tracks initial order
Random
- Idea: randomly select one of the blocks in the cache to evict
- Works with low temporal locality of workload
MRU (Most Recently Used), aka fetch-and-discard
- Idea: select the block that has been used most recently of all the block

Average Memory Access Time (AMAT)

Performance model:

Minimize: AMAT = Hit Time + Miss Penalty * Miss Rate

Improving Miss Penalty: Multi-level Cache Hierarchy

In today's 3 GHz Processor and 80 ns to go to DRAM = ~200 processor clock cycles Solution: Second Level (L2) Cache

L1 Miss Penalty = L2 Hit Time + L2 Miss Rate * L2 Miss Penalty
AMAT = L1 Hit Time + L1 Miss Rate * (L2 Hit Time + L2 Miss Rate * L2 Miss Penalty)

Reduce Miss Rate

Larger cache
- Limited by cost and tech
- Hit time of L1 Cache need to < Cycle time (bigger caches are slower)
Associativity - More places in the cache to put each block of memory

Typical Scale

L1
- size: tens of KB
- hit time: complete in one clock cycle
- miss rates: 1-5%
L2:
- size: hundreds of KB
- hit time: few clock cycles
- miss rates: 10-20%
L2 miss rate is fraction of L1 misses that also miss in L2

Caches ​

Memory Hierarchy ​

Memory Caching ​

Cache Locality, Design, Management ​

Locality ​

Cache Design ​

Managing Memory Hierarchy ​

Effect of Caching ​

Direct Mapped Caches ​

Terminlogy ​

Memory Access with Cache ​

Caching Terminology ​

Example: Multiword-Block Direct-Mapped Cache ​

Cache Write Policy ​

Block Size Tradeoff ​

Types of Cache Misses ​

Fully Associative Caches ​

(N-Way) Set-Associative Caches ​

Block Replacement ​

Replacement Policy ​

Average Memory Access Time (AMAT) ​

Improving Miss Penalty: Multi-level Cache Hierarchy ​

Reduce Miss Rate ​

Typical Scale ​