9.3 三重积分的计算
直角坐标系下的计算
柱线法
若
将三重积分化为下限为
截面法
区域
后续的二重积分分别求出
三重积分的变量代换
柱面坐标系下的计算
柱面坐标系
设点
柱面坐标变换
柱线法:
截面法:
球面坐标系下的计算
球面坐标系
设点
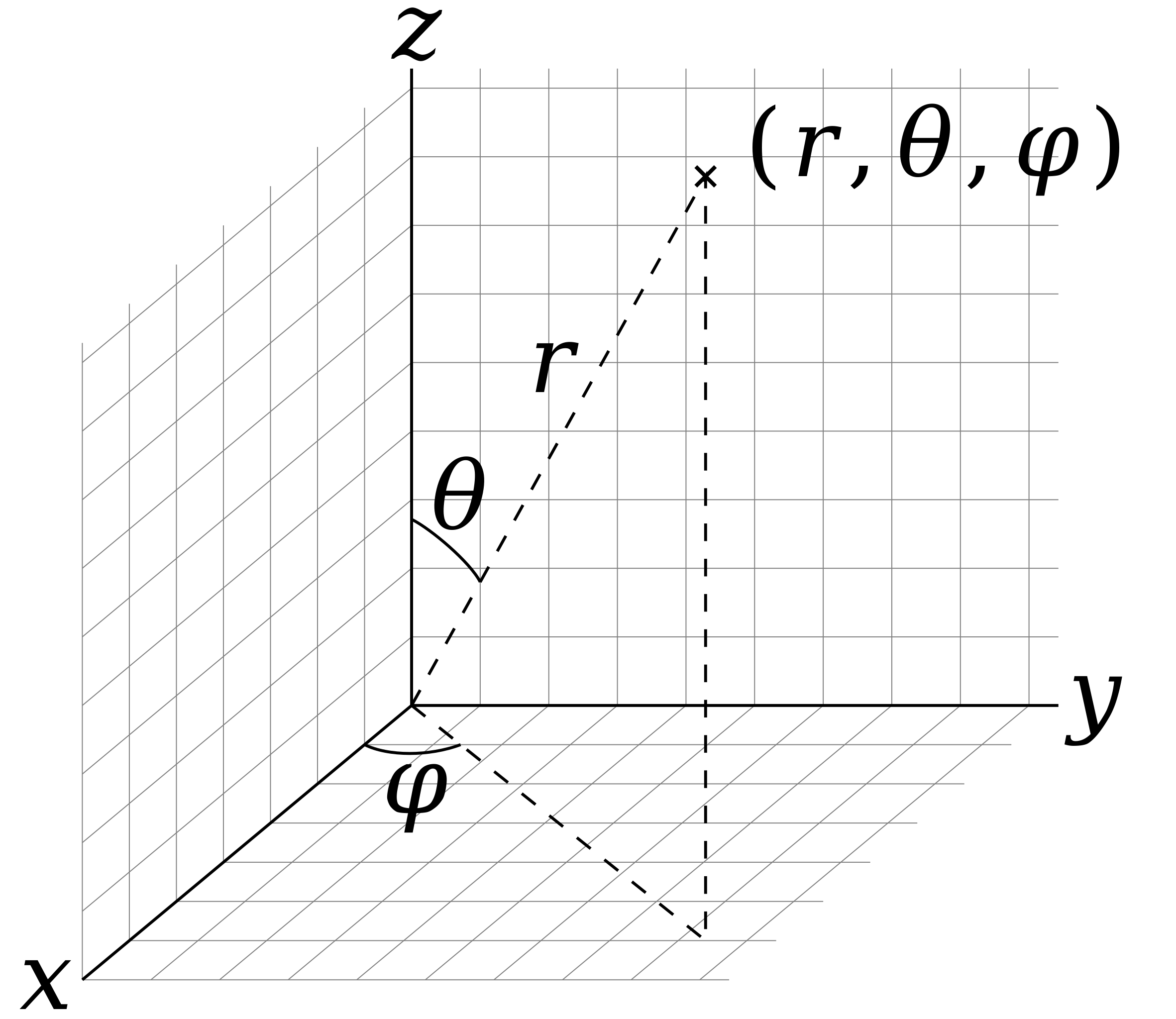
球面坐标变换
何时应用球坐标变换
当被积函数或积分区域包含类似于
带系数的形式可以采用广义球面坐标变换
若
将三重积分化为下限为
区域
后续的二重积分分别求出
设点
柱面坐标变换
柱线法:
截面法:
设点

球面坐标变换
当被积函数或积分区域包含类似于
带系数的形式可以采用广义球面坐标变换